Rumus Phytagoras Beserta Contoh Soalnya

RUMUS PHYTAGORAS BESERTA CONTOH SOALNYA

Rumus Phytagoras

Perhatikan contoh permasalahan dalam bentuk gambar di bawah ini.

Permasalahan tentang Rumus Phytagoras

Misalkan terdapat sebuah bangunan dengan tinggi 4 m dan sebuah tangga dengan panjang 5 m. Jika tangga tersebut akan disandarkan pada bangunan tersebut dengan ujung tangga terletak pada ujung bangunan seperti gambar di atas, dapatkah kalian menentukan jarak bangunan tersebut dengan bagian pangkal tangga? Tahukah kalian rumus apa yang kita gunakan untuk menentukan jarak tersebut dan bagaimana cara mengerjakannya? Nah, untuk menjawab pertanyaan tersebut, mari kita pelajari bersama materi ini dengan baik.

Rumus Phytagoras

Rumus Phytagoras adalah sebuah rumus yang didapati dari penginterpretasian teorema Phytagoras. Teorema Phytagoras sendiri merupakan teorema yang dikemukakan oleh seorang matematikiawan Yunani yang bernama Phytagoras. Adapun isi dari teorema Phytagoras antara lain sebagai berikut.

Pada sebuah segitiga siku-siku, kuadrat dari sisi terpanjang adalah sama dengan hasil jumlah dari kuadrat sisi-sisi penyikunya.

Dari isi teorema tersebut, maka misalkan kita punya sebuah segitiga siku-siku ABC dengan siku-siku di B dan sisi terpanjangnya adalah sisi AC yang digambarkan sebagai berikut.

Segitiga Siku-siku ABC

Selanjutnya sesuai dengan isi teorema Phytagoras, maka dapat dapat dibuat rumus sebagai berikut.

Rumus Phytagoras

Rumus tersebut biasa digunakan untuk menunjukkan apakah sebuah segitiga termasuk dalam segitiga siku-siku atau bukan. Nah, untuk mempermudah dalam memahami pernyataan tersebut, maka cermatilah contoh soal di bawah ini.

Contoh 1:

Seorang guru matematika meminta siswanya untuk menggambar sebuah segitiga dengan panjang sisi 7 cm, 24 cm, dan 25 cm. Menurut kalian, apakah segitiga yang digambar oleh siswa tersebut adalah segitiga siku-siku?

Penyelesaian:

Dari permasalahan di atas didapati bahwa sisi terpanjang segitiga tersebut memiliki panjang yaitu 25 cm. Untuk menunjukkan bahwa segitiga tersebut adalah segitiga siku-siku sesuai dengan rumus Phytagoras, maka kita harus menunjukkan bahwa 25² = 7² + 24²

25²             =  625

7² + 24²     =  49 + 576

                   =  625

Dari perhitungan di atas, didapati bahwa  25² = 7² + 24². Oleh karena itu, kita bisa menyimpulkan bahwa segitiga yang digambar siswa adalah segitiga siku-siku.

Cara Menentukan Panjang Sisi Pada Segitiga Siku-Siku

Pada penjelasan sebelumnya, kita sudah mengetahui bahwa rumus Phytagoras dapat digunakan untuk menentukan apakah sebuah segitiga termasuk dalam segitiga siku-siku atau bukan. Nah selain hal itu, rumus Phytagoras juga dapat digunakan untuk menentukan panjang sisi pada segitiga siku-siku. Caranya bagaimana? Untuk lebih jelasnya, mari kita pelajari bersama sub materi berikut ini.

Menentukan Panjang Sisi Terpanjang Segitiga Siku-Siku

Untuk menentukan panjang sisi terpanjang dari sebuah segitiga siku-siku, maka kita harus melakukan pengakaran terhadap penjumlahan dari kuadrat masing-masing sisi yang bukan merupakan sisi terpanjang. Penjelasan itu dapat kita pahami dari hal berikut ini.

Misalkan dipunya sebuah segitiga siku-siku ABC dengan siku-siku di B yang digambarkan sebagai berikut.

Segitiga Siku-siku ABC

Dari gambar di atas diketahui bahwa sisi terpanjang segitiga siku-siku ABC adalah sisi AC. Jadi, untuk menentukan panjang sisi AC dapat dilakukan dengan rumus:

Rumus Sisi Terpanjang

Agar kalian lebih mudah dalam memahami rumus tersebut, coba pahamilah contoh soal di bawah ini.

Contoh 1:

Diketahui sebuah segitiga siku-siku KLM dengan siku-siku di L yang digambarkan sebagai berikut.

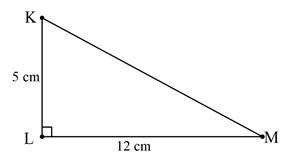Segitiga Siku-siku KLM

Tentukan panjang sisi KM dari segitiga siku-siku tersebut!

Penyelesaian:

Diketahui:

KL = 5 cm

LM = 12 cm

Ditanya:

KM = ………..?

Jawab:

KM adalah sisi terpanjang pada segitiga siku-siku KLM. Dengan demikian, untuk menentukan panjang KM digunakan rumus:

KM         =  √(KL² + LM²)

               =  √(5² + 12²)

               =  √(25 + 144)

               =  √(169)

               =  13

Jadi, panjang sisi KM pada segitiga siku-siku KLM adalah 13 cm.

Contoh 2:

Sebuah segitiga siku-siku PQR dengan siku-siku di Q digambarkan sebagai berikut.

Segitiga Siku-siku PQR

Tentukan panjang sisi PR dari segitiga siku-siku tersebut!

Penyelesaian:

Diketahui:

PQ = 24 cm

QR = 7 cm

Ditanya:

PR = ………..?

Jawab:

PR adalah sisi terpanjang pada segitiga siku-siku PQR. Dengan demikian, untuk menentukan panjang PR digunakan rumus:

PR          =  √(PQ² + QR²)

               =  √(24² + 7²)

               =  √(576 + 49)

               =  √(625)

               =  25

Jadi, panjang sisi PR pada segitiga siku-siku PQR adalah 25 cm.

Menentukan Panjang Sisi Yang Bukan Sisi Terpanjang Segitiga Siku-Siku

Pada sebuah segitiga siku-siku, kita mengenal adanya sebuah sisi yang berukuran paling panjang dan dua sisi yang bukan merupakan sisi terpanjang. Nah untuk menentukan panjang sisi segitiga siku-siku yang bukan merupakan sisi terpanjang, maka kita harus melakukan pengakaran terhadap hasil pengurangan kuadrat sisi terpanjang dikurangkan dengan kuadrat sisi lainnya yang bukan merupakan sisi terpanjang. Penjelasan itu dapat kita pahami dari hal berikut ini.

Misalkan dipunya sebuah segitiga siku-siku ABC dengan siku-siku di B yang digambarkan sebagai berikut.

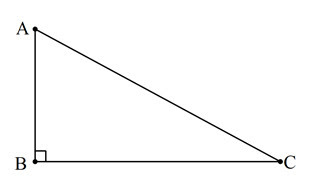Segitiga Siku-siku ABC

Pada gambar segitiga siku-siku ABC di atas, didapati bahwa sisi AC merupakan sisi terpanjang dan sisi AB dan BC bukan merupakan sisi terpanjang. Dengan demikian sesuai dengan pernyataan di atas bahwa untuk menentukan sisi yang bukan sisi terpanjang yaitu sisi AB dapat dilakukan dengan menggunakan rumus:

Rumus Sisi Bukan Terpanjang

Sedangkan untuk menentukan sisi yang bukan merupakan sisi terpanjang BC dapat dilakukan dengan rumus berikut:

Rumus Sisi Bukan Terpanjang

Untuk mempermudah kalian dalam memahami kedua rumus tersebut, mari kita coba pelajari contoh soal berikut ini.

Contoh 1:

Diketahui sebuah segitiga siku-siku ABC dengan siku-siku di B yang digambarkan sebagai berikut.

Segitiga Siku-siku ABC

Tentukan panjang sisi AB dari segitiga siku-siku tersebut!

Penyelesaian:

Diketahui:

BC = 4 cm

AC = 5 cm

Ditanya:

AB = ………..?

Jawab:

AB merupakan salah satu sisi dari segitiga siku-siku ABC tetapi bukan merupakan sisi yang terpanjang. Dengan demikian, untuk menentukan panjang sisi AB dapat digunakan rumus:

AB          =  √(AC² – BC²)

               =  √(5² – 4²)

               =  √(25 – 16)

               =  √(9)

               =  3

Jadi, panjang sisi AB pada segitiga siku-siku ABC adalah 3 cm.

Contoh 2:

Sebuah segitiga siku-siku MNO dengan siku-siku di N digambarkan sebagai berikut.

Segitiga Siku-siku MNO

Tentukan panjang sisi NO dari segitiga siku-siku tersebut!

Penyelesaian:

Diketahui:

MN = 8 cm

MO = 17 cm

Ditanya:

NO = ………..?

Jawab:

NO merupakan salah satu sisi dari segitiga siku-siku MNO tetapi bukan merupakan sisi yang terpanjang. Dengan demikian, untuk menentukan panjang sisi NO dapat dilakukan dengan rumus:

NO         =  √(MO² – MN²)

               =  √(17² – 8²)

               =  √(289 – 64)

               =  √(225)

               =  15

Jadi, panjang sisi NO pada segitiga siku-siku MNO adalah 15 cm.

Demikian penjelasan terkait rumus Phytagoras. Somoga materi ini bisa memberikan manfaat untuk kalian semua.