Perbandingan Trigonometri Pada Segitiga Siku-Siku

PERBANDINGAN TRIGONOMETRI PADA SEGITIGA SIKU-SIKU 

Perbandingan Trigonometri Pada Segitiga Siku-Siku

Trigonometri merupakan salah satu cabang ilmu matematika yang mempelajari tentang sudut, sisi, dan perbandingan diantara sudut dan sisi pada sebuah segitiga. Perbandingan trigonometri berarti kita melakukan pembandingan antar sudut, sisi, atau sudut dan sisi dari sebuah segitiga.

Nah, karena materi yang akan kita bahas adalah perbandingan trigonometri pada segitiga siku-siku, berarti secara spesifik pembandingan-pembandingan itu akan dilakukan pada sebuah segitiga siku-siku.

Seperti kita ketahui bahwa segitiga siku-siku adalah sebuah segitiga yang salah satu sudutnya berbentuk siku-siku atau memiliki besar sudut 90^o. Sama seperti segitiga lainnya, segitiga siku-siku juga memiliki tiga sisi. Nah, ketiga sisi inilah yang akan kita bandingkan pada materi kali ini.

Selanjutnya, untuk memudahkan dalam melakukan pembandingan tadi, maka kita perlu menamai setiap sisi pada segitiga siku-siku. Misalkan dipunyai segitiga siku-siku ABC dengan siku-siku di B. Selain sudut siku di B, ada sudut lain yang diketahui yaitu sudut 𝛼 sebagai acuannya. Adapun penggambaran dari segitiga siku-siku tersebut antara lain sebagai berikut.

Segitiga Siku-Siku ABC dengan Siku-Siku di B

Penamaan sisi-sisi pada segitiga siku-siku di atas dapat dilakukan dengan cara sebagai berikut.

Sisi Depan, sisi depan atau disingkat dengan “De” adalah sisi yang terlatak berhadapan dengan sudut acuan yang dimaksud pada sebuah segitiga siku-siku.

Pada segitiga siku-siku ABC di atas, diketahui yang menjadi sudut acuan adalah sudut 𝛼 sehingga yang dimaksud sebagai sisi depan adalah sisi yang berhadapan dengan sudut acuan tersebut yaitu sudut 𝛼. Dengan kata lain, sisi depan yang dimaksud disini adalah sisi AB.

Sisi Miring, sisi miring atau disingkat dengan “Mi” adalah sisi terpanjang pada sebuah segitiga siku-siku.

Pada segitiga siku-siku ABC di atas dengan sudut acuan yang diketahui adalah sudut 𝛼, yang dimaksud sebagai sisi miring adalah sisi terpanjang dari segitiga siku-siku tersebut. Dengan demikian, sisi miring yang dimaksud adalah sisi AC.

Sisi Samping, sisi samping atau disingkat “Sa” adalah sisi pada sebuah segitiga siku-siku yang bukan merupakan sisi terpanjang dan bukan merupakan sisi yang terletak berhadapan dengan sudut acuan yang dimaksud. 

Pada segitiga siku-siku ABC di atas dengan sudut acuan yang diketahui adalah sudut 𝛼, yang dimaksud sebagai sisi samping adalah sisi yang bukan merupakan sisi terpanjang dan bukan merupakan sisi yang berhadapan dengan sudut acuan 𝛼. Dengan demikian, sisi samping yang dimaksud adalah sisi BC.

Perbandingan Trigonometri Pada Segitiga Siku-Siku

Setelah kita menamai sisi-sisi pada segitiga siku-siku ABC dengan siku-siku di B dan diketahui sudut lain yang menjadi acuan yaitu sudut 𝛼, maka kita dapat menggambarkan segitiga yang sudah dinamai tersebut dalam bentuk sebagai berikut.

Segitiga Siku-Siku ABC dengan Siku-Siku di B

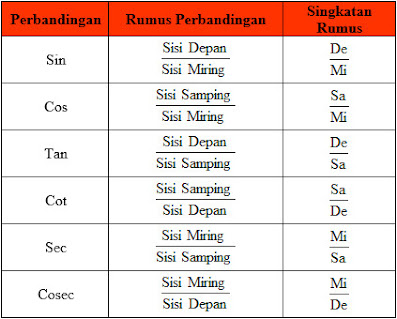
Sesuai dengan gambar di atas, maka perbandingan sisi-sisi pertama yang bisa kita lakukan adalah sisi depan dibanding sisi miring atau bisa kita tuliskan (Sisi Depan)/(Sisi Miring) atau De/Mi. Perbandingan ini biasa dikenal dengan istilah “sinus” atau disingkat menjadi “sin”. Nah, karena acuan dalam penentuan sisi depan dan sisi miring adalah sudut 𝛼, maka penulisan “sin” tadi harus diikuti dengan sudut acuan tersebut. Dengan demikian, kita menuliskannya dalam bentuk sin 𝛼.

Dari penjelasan tersebut, maka untuk menentukan nilai sin 𝛼 pada segitiga siku-siku ABC di atas dapat menggunakan rumus sebagai berikut. 

Rumus Sin

Perbandingan kedua yang dapat kita lakukan terhadap sisi-sisi segitiga siku-siku adalah sisi samping dibanding sisi miring atau bisa kita tuliskan (Sisi Samping)/(Sisi Miring) atau Sa/Mi. Perbandingan ini biasa dikenal dengan istilah “cosinus” atau disingkat menjadi “cos”. Nah, karena acuan dalam penentuan sisi samping dan sisi miring adalah sudut 𝛼, maka penulisan “cos” tadi harus diikuti dengan sudut acuan tersebut. Dengan demikian, kita menuliskannya dalam bentuk cos 𝛼.

Dari penjelasan tersebut, maka untuk menentukan nilai cos 𝛼 pada segitiga siku-siku ABC di atas dapat menggunakan rumus sebagai berikut. 

Rumus Cos

Perbandingan ketiga yang dapat kita lakukan adalah sisi depan dibanding sisi samping atau bisa kita tuliskan (Sisi Depan)/(Sisi Samping) atau De/Sa. Perbandingan ini biasa dikenal dengan istilah “tangent” atau disingkat menjadi “tan”. Nah, karena acuan dalam penentuan sisi depan dan sisi samping adalah sudut 𝛼, maka penulisan “tan” tadi harus diikuti dengan sudut acuan tersebut. Dengan demikian, kita menuliskannya dalam bentuk tan 𝛼.

Dari penjelasan tersebut, maka untuk menentukan nilai tan 𝛼 pada segitiga siku-siku ABC di atas dapat menggunakan rumus sebagai berikut.

Rumus Tan

Perbandingan keempat yang dapat kita lakukan pada sisi segitiga siku-siku adalah sisi samping dibanding sisi depan atau bisa kita tuliskan (Sisi Samping)/(Sisi Depan) atau Sa/De. Perbandingan ini biasa dikenal dengan istilah “cotangent” atau disingkat menjadi “cot”. Nah, karena acuan dalam penentuan sisi samping dan sisi depan adalah sudut 𝛼, maka penulisan “cot” tadi harus diikuti dengan sudut acuan tersebut. Dengan demikian, kita menuliskannya dalam bentuk cot 𝛼.

Dari penjelasan tersebut, maka untuk menentukan nilai cot 𝛼 pada segitiga siku-siku ABC di atas dapat menggunakan rumus sebagai berikut.

Rumus Cot

Perbandingan kelima yang dapat kita lakukan adalah sisi miring dibanding sisi samping atau bisa kita tuliskan (Sisi Miring)/(Sisi Samping) atau Mi/Sa. Perbandingan ini biasa dikenal dengan istilah “secant” atau disingkat menjadi “sec”. Nah, karena acuan dalam penentuan sisi miring dan sisi samping adalah sudut 𝛼, maka penulisan “sec” tadi harus diikuti dengan sudut acuan tersebut. Dengan demikian, kita menuliskannya dalam bentuk sec 𝛼.

Dari penjelasan tersebut, maka untuk menentukan nilai sec 𝛼 pada segitiga siku-siku ABC di atas dapat menggunakan rumus sebagai berikut.

Rumus Sec

Perbandingan keenam yang dapat kita lakukan adalah sisi miring dibanding sisi depan atau bisa kita tuliskan (Sisi Miring)/(Sisi Depan) atau Mi/De. Perbandingan ini biasa dikenal dengan istilah “cosecant” atau disingkat menjadi “cosec”. Nah, karena acuan dalam penentuan sisi miring dan sisi depan adalah sudut 𝛼, maka penulisan “cosec” tadi harus diikuti dengan sudut acuan tersebut. Dengan demikian, kita menuliskannya dalam bentuk cosec 𝛼.

Dari penjelasan tersebut, maka untuk menentukan nilai cosec 𝛼 pada segitiga siku-siku ABC di atas dapat menggunakan rumus sebagai berikut.

Rumus Cosec

Demikian perbandingan-perbandingan yang dapat kita buat dari sisi-sisi segitiga siku-siku. Berikut adalah tabel kumpulan perbandingan trigonometri pada segitiga siku-siku yang barusan kita bahas di atas.

Tabel Rumus Perbandingan Trigonometri

Untuk mempermudah dalam memahami rumus-rumus di atas, marilah kita pelajari beberapa contoh soal di bawah ini.

Contoh 1:

Diberikan sebuah segitiga siku-siku ABC dengan siku-siku di B berikut ini.

Segitiga ABC

Tentukan nilai dari perbandingan trigonometri berikut:

1.      sin 𝛼

2.      cos 𝛼

3.      tan 𝛼

4.      cot 𝛼

5.      sec 𝛼

6.      cosec 𝛼

Penyelesaian:

Untuk menentukan perbandingan trigonometri dari sebuah segitiga siku-siku, maka langkah pertama yang harus dilakukan adalah menentukan sisi depan, sisi miring, dan sisi samping dari segitiga siku-siku tersebut yang digambarkan sebagai berikut.

Segitiga ABC

Dari gambar di atas maka didapati:

Sisi Depan : De = 3 cm;

Sisi Miring : Mi = 5 cm;

Sisi Samping : Sa = 4 cm.

Dengan demikian didapati perbandingan trigonometri sebagai berikut:

1.      sin 𝛼                =  De/Mi  =  3/5

2.      cos 𝛼               =  Sa/Mi  =  4/5

3.      tan 𝛼               =  De/Sa  =  3/4

4.      cot 𝛼               =  Sa/De  =  4/3

5.      sec 𝛼               =  Mi/Sa  =  5/4

6.      cosec 𝛼           =  Mi/De  =  5/3

Contoh 2:

Diberikan sebuah segitiga siku-siku PQR dengan siku-siku di Q berikut ini.

Segitiga PQR

Tentukan nilai dari perbandingan trigonometri berikut:

1.      sin 𝛽

2.      cos 𝛽

3.      tan 𝛽

4.      cot 𝛽

5.      sec 𝛽

6.      cosec 𝛽

Penyelesaian:

Untuk menentukan sin, cos, tan, cot, sec, dan cosec di atas, kita menggunakan sudut acuan 𝛽. Dengan demikian dalam penentuan sisi depan, sisi miring, dan sisi samping, kita juga mengacu pada sudut 𝛽.

Segitiga PQR

Dari gambar di atas maka didapati:

Sisi Depan : De = 24 cm;

Sisi Miring : Mi = 25 cm;

Sisi Samping : Sa = 7 cm.

Dengan demikian didapati perbandingan trigonometri sebagai berikut:

1.      sin 𝛽                 =  De/Mi  =  24/25

2.      cos 𝛽                =  Sa/Mi  =  7/25

3.      tan 𝛽                =  De/Sa  =  24/7

4.      cot 𝛽                =  Sa/De  =  7/24

5.      sec 𝛽                =  Mi/Sa  =  25/7

6.      cosec 𝛽            =  Mi/De  =  25/24

Contoh 3:

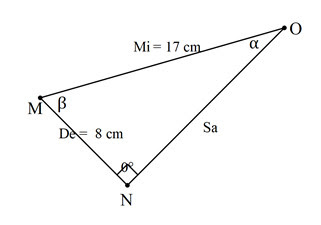
Diberikan sebuah segitiga siku-siku MNO dengan siku-siku di N berikut ini.

Segitiga MNO

Tentukan nilai dari perbandingan trigonometri dari cos 𝛼 !

Penyelesaian:

Sebelum kita menentukan nilai perbandingan trigonometri cos 𝛼, maka kita harus menentukan terlebih dahulu sisi depan, sisi miring, dan sisi samping dari segitiga siku-siku tersebut. Karena yang ditanyakan adalah cos 𝛼, maka yang menjadi sudut acuan dalam penentuan sisi depan, sisi miring, dan sisi samping adalah sudut 𝛼.

Segitiga MNO

Karena yang kita cari adalah nilai cos 𝛼, maka untuk menentukan nilai cos 𝛼 tersebut digunakan rumus Sa/Mi. Selanjutnya, karena sisi samping (Sa) belum diketahui, maka kita harus menentukan terlebih dahulu panjang sisi samping dengan menggunakan rumus Phytagoras.

Sisi samping (Sa) merupakan salah satu sisi dari segitiga siku-siku MNO tetapi bukan merupakan sisi yang terpanjang. Dengan demikian, untuk menentukan panjang sisi samping (Sa) dapat dilakukan dengan rumus:

Sa           =  √(Mi² – De²)

               =  √(17² – 8²)

               =  √(289 – 64)

               =  √(225)

               =  15

Jadi, panjang sisi samping (Sa) pada segitiga siku-siku MNO adalah 15 cm dan segitiga siku-siku MNO dapat digambarkan ulang sebagai berikut.

Segitiga MNO

Dengan demikian nilai perbandingan cos 𝛼 dapat ditentukan ditentukan yaitu:

cos 𝛼  =  Sa/Mi  =  15/17.

Demikian penjelasan terkait materi perbandingan trigonometri pada segitiga siku-siku. Semoga penjelasan ini dapat bermanfaat untuk semua.