Perbandingan Trigonometri Pada Sudut Istimewa

PERBANDINGAN TRIGONOMETRI PADA SUDUT ISTIMEWA 

Tabel Nilai Perbandingan Trigonometri Sudut Istimewa

Perbandingan trigonomoteri adalah perbandingan yang dilakuan terhadap sisi-sisi pada sebuah segitiga. Perbandingan ini dilakukan dengan tujuan untuk menentukan nilai perbandingan yang berdasarkan pada suatu sudut acuan tertentu.

Dalam trigonometri, kita mengenal ada beberapa sudut yang dikatakan sebagai sudut istimewa. Mengapa demikian? Hal ini dikarenakan sudut-sudut tersebut memiliki nilai perbandingan trigonometri yang dapat ditentukan secara eksak, tanpa menggunakan kalkulator atau tabel matematika. Beberapa diantaranya adalah 0^o, 30^o, 45^o, 60^o, dan 90^o.

Nah, sudut-sudut itulah yang akan kita pelajari berapa nilai perbandingannya dan bagaimana caranya untuk mendapatkan nilai tersebut. Untuk lebih jelasnya, mari kita pelajari bersama pembahasan di bawah ini.

Perbandingan Trigonometri Untuk Sudut 30^o

Untuk menunjukkan nilai perbandingan trigonometri pada sudut 30^o, maka langkah pertama yang perlu kita lakukan adalah menggambarkan sebuah segitiga sama sisi yang memiliki panjang sisi yaitu 2 satuan yang digambarkan sebagai berikut.

Segitiga Sama Sisi

Nah, untuk mendapatkan sudut 30^o, maka kita bagi segitiga sama sisi di atas menjadi dua bagian yang sama besar sesuai dengan sumbu simetrinya yang digambarkan sebagai berikut.

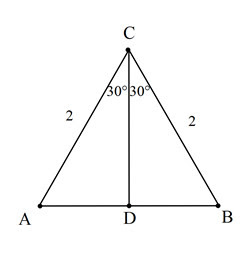Segitiga Sama Sisi Dibagi Berdasar Sumbu Simetri

Setelah itu, kita pilih salah satu bagian yaitu segitiga siku-siku ADC dengan siku-siku di D dan sudut C dengan besar 30^o dijadikan sebagai sudut acuan yang digambarkan sebagai berikut.

Untuk menentukan perbandingan trigonometri dari sudut acuan 30^o di atas, kita dapat memanfaatkan konsep perbandingan trigonometri pada segitiga siku-siku. Oleh karena itu, kita harus menentukan terlebih dahulu sisi depan, sisi miring, dan sisi samping dari segitiga itu yang digambarkan sebagai berikut.

Segitiga ADC

Karena sisi samping (Sa) belum diketahui nilainya, maka kita tentukan nilai sisi samping terlebih dahulu dengan menggunakan rumus Phytagoras.

Sa           =  \(\sqrt{Mi^{2}-De^{2}}\)

               =  \(\sqrt{2^{2}-1^{2}}\)

               =  \(\sqrt{4 - 1}\)

               =  \(\sqrt{3}\)

Jadi, panjang sisi samping (Sa) pada segitiga siku-siku ADC adalah \(\sqrt{3}\) satuan dan segitiga siku-siku ADC dapat digambarkan ulang sebagai berikut.

Segitiga ADC

Dari gambar segitiga siku-siku ADC di atas, maka kita dapat menentukan nilai perbandingan trigonometri untuk sudut acuan 30^o yaitu:

1.      sin 30^o           = \(\frac{De}{Mi}=\frac{1}{2}\)

2.      cos 30^o          =  \(\frac{Sa}{Mi}=\frac{1}{2}\sqrt{3}\)

3.      tan 30^o          =  \(\frac{De}{Sa}=\frac{1}{3}\sqrt{3}\)

4.      cot 30^o          =  \(\frac{Sa}{De}=\sqrt{3}\)

5.      sec 30^o          =  \(\frac{Mi}{Sa}=\frac{2}{3}\sqrt{3}\)

6.      cosec 30^o      =  \(\frac{Mi}{De}= 2\)

Perbandingan Trigonometri Untuk Sudut 60^o

Sama halnya dengan sudut 30^o, langkah pertama yang harus kita lakukan untuk menunjukkan nilai perbandingan trigonometri pada sudut 60^o adalah dengan menggambarkan terlebih dahulu segitiga sama sisi yang memiliki panjang sisi yaitu 2 satuan yang digambarkan sebagai berikut.

Segitiga ABC

Nah, agar kita lebih mudah dalam melakukan perhitungan, kita bagi segitiga tersebut menjadi dua bagian yang sama besar sesuai dengan sumbu simetrinya yang digambarkan sebagai berikut.

Segitiga ABC

Selanjutnya kita pilih salah satu bagian yaitu segitiga siku-siku ADC dengan siku-siku di D dan acuannya adalah sudut A dengan besar 60^o. Adapun penggambarannya adalah:

Segitiga ADC

Untuk menentukan perbandingan trigonometri dari sudut acuan 60^o di atas, kita dapat memanfaatkan konsep perbandingan trigonometri pada segitiga siku-siku. Oleh karena itu, kita harus menentukan terlebih dahulu sisi depan, sisi miring, dan sisi samping dari segitiga itu. Adapaun penentuan sisi-sisi tersebut dapat digambarkan sebagai berikut.

Segitiga ADC

Karena sisi depan (De) belum diketahui nilainya, maka kita tentukan nilai sisi depan terlebih dahulu dengan menggunakan rumus Phytagoras.

De           =   \(\sqrt{Mi^{2}-Sa^{2}}\)

               =   \(\sqrt{2^{2}-1^{2}}\)

               =   \(\sqrt{4 - 1}\)

               =   \(\sqrt{3}\)

Jadi, panjang sisi depan (De) pada segitiga siku-siku ADC adalah \(\sqrt{3}\) satuan dan segitiga siku-siku ADC dapat digambarkan ulang sebagai berikut.

Segitiga ADC

Dari gambar segitiga siku-siku ADC di atas, maka kita dapat menentukan nilai perbandingan trigonometri untuk sudut acuan 60^o yaitu:

1.      sin 60^o           =  \(\frac{De}{Mi} = \frac{1}{2}\sqrt{3}\)

2.      cos 60^o          =  \(\frac{Sa}{Mi} = \frac{1}{2}\)

3.      tan 60^o          =  \(\frac{De}{Sa} = \sqrt{3}\)

4.      cot 60^o          =  \(\frac{Sa}{De} = \frac{1}{3}\sqrt{3}\)

5.      sec 60^o          =  \(\frac{Mi}{Sa} = 2\)

6.      cosec 60^o      =  \(\frac{Mi}{De} = \frac{2}{3}\sqrt{3}\)

Perbandingan Trigonometri Untuk Sudut 45^o

Dalam menunjukkan nilai perbandingan trigonometri untuk sudut 45^o, langkah pertama yang bisa kita lakukan adalah menggambarkan segitiga sama kaki dimana salah satu sudutnya adalah sudut siku-siku dengan panjang kakinya adalah 1 satuan yang digambarkan sebagai berikut.

Segitiga ABC

Selanjutnya, untuk menentukan perbandingan trigonometri dari sudut acuan 45^o di atas, kita dapat memanfaatkan konsep perbandingan trigonometri pada segitiga siku-siku. Oleh karena itu, kita harus menentukan terlebih dahulu sisi depan, sisi miring, dan sisi samping dari segitiga itu. Adapaun penentuan sisi-sisi tersebut dapat digambarkan sebagai berikut.

Segitiga ABC

Karena sisi miring (Mi) belum diketahui nilainya, maka kita tentukan nilai sisi miring terlebih dahulu dengan menggunakan rumus Phytagoras.

Mi           =   \(\sqrt{De^{2}+Sa^{2}}\)

               =   \(\sqrt{1^{2}+1^{2}}\)

               =   \(\sqrt{1 + 1}\)

               =   \(\sqrt{2}\)

Jadi, panjang sisi miring (Mi) pada segitiga siku-siku ABC adalah \(\sqrt{2}\) satuan dan segitiga siku-siku ABC dapat digambarkan ulang sebagai berikut.

Segitiga ABC

Dari gambar segitiga siku-siku ABC di atas, maka kita dapat menentukan nilai perbandingan trigonometri untuk sudut acuan 45^o yaitu:

1.      sin 45^o           =  \(\frac{De}{Mi}\)

                               =  \(\frac{1}{\sqrt{2}}\)

                               =  \(\frac{1}{\sqrt{2}}\times\frac{\sqrt{2}}{\sqrt{2}}\)

                               =  \(\frac{1}{2}\sqrt{2}\)

2.      cos 45^o          =  \(\frac{Sa}{Mi}\)

                               =  \(\frac{1}{\sqrt{2}}\)

                               =  \(\frac{1}{\sqrt{2}}\times\frac{\sqrt{2}}{\sqrt{2}}\)

                               =  \(\frac{1}{2}\sqrt{2}\)

3.      tan 45^o          =  \(\frac{De}{Sa}\)

                               =  \(\frac{1}{1}\)

                               =  1

4.      cot 45^o          =  \(\frac{Sa}{De}\)

                               =  \(\frac{1}{1}\)

                               =  1

5.      sec 45^o          =  \(\frac{Mi}{Sa}\)

                               =  \(\frac{\sqrt{2}}{1}\)

                               =  \(\sqrt{2}\)

6.      cosec 45^o       =  \(\frac{Mi}{De}\)

                               =  \(\frac{\sqrt{2}}{1}\)

                               =  \(\sqrt{2}\)

Perbandingan Trigonometri Untuk Sudut 0^o

Untuk menentukan nilai perbandingan pada sudut 0^o, maka kita akan menggunakan konsep berikut.

Koordinat Kartesius

Selanjutnya kita gambarkan garis r dengan panjang 1 satuan dan 𝜗 = 0^o sebagai berikut.

Koordinat Kartesius

Dari gambar tersebut maka didapati yaitu:

r     =  Sisi Miring  =  Mi  =  1

y    =  Sisi Depan  =  De  =  0

x    =  Sisi Samping  =  Sa  = 1

Sehingga kita dapat menentukan nilai perbandingan trigonometri untuk sudut 0^o sebagai berikut.

1.      sin 0^o             =  \(\frac{De}{Mi}=\frac{0}{1}=0\)

2.      cos 0^o            =  \(\frac{Sa}{Mi}=\frac{1}{1}=1\)

3.      tan 0^o            =  \(\frac{De}{Sa}=\frac{0}{1}=0\)

3.      cot 0^o            =  \(\frac{Sa}{De}=\frac{1}{0}=\)Tidak Terdefinisi

5.      sec 0^o            =  \(\frac{Mi}{Sa}=\frac{1}{1}=1\)

6.      cosec 0^o        =  \(\frac{Mi}{De}=\frac{1}{0}=\) Tidak terdefinisi

Perbandingan Trigonometri Untuk Sudut 90^o

Untuk menentukan nilai perbandingan pada sudut 90^o, maka kita akan menggunakan konsep berikut.

Koordinat Kartesius

Selanjutnya kita gambarkan garis r dengan panjang 1 satuan dan 𝜗 = 90^o sebagai berikut.

Koordinat Kartesius

Dari gambar tersebut maka didapati yaitu:

r     =  Sisi Miring  =  Mi  =  1

y    =  Sisi Depan  =  De  =  1

x    =  Sisi Samping  =  Sa  = 0

Sehingga kita dapat menentukan nilai perbandingan trigonometri untuk sudut 90^o sebagai berikut.

1.      sin 90^o           =  \(\frac{De}{Mi}=\frac{1}{1}=1\)

2.      cos 90^o          =  \(\frac{Sa}{Mi}=\frac{0}{1}=0\)

3.      tan 90^o          =  \(\frac{De}{Sa}=\frac{1}{0}=\) Tidak terdefinisi

4.      cot 90^o          =  \(\frac{Sa}{De}=\frac{0}{1}=0\)

5.      sec 90^o          =  \(\frac{Mi}{Sa}=\frac{1}{0}=\) Tidak Terdefinisi

6.      cosec 90^o      =  \(\frac{Mi}{De}=\frac{1}{1}=1\)

Dari berbagai penjelasan di atas, maka kita dapat membuat sebuah tabel nilai perbandingan trigonometri pada sudut istimewa sebagai berikut.

Tabel Hasil Perbandingan Trigonometri Pada Sudut Istimewa

Untuk memahami penjelasan dan tabel yang sudah kita buat di atas, silahkan kalian cermati beberapa contoh soal di bawah ini.

Contoh 1:

Sebuah segitiga siku-siku ABC dengan siku-siku di B digambarkan sebagai berikut.

Segitiga ABC

Tentukan panjang sisi AC!

Penyelesaian:

Diketahui:

AB  =  6 cm;

Besar ∠ACB = 30^o.

Ditanya:

AC = ………..?

Jawab:

Sebelum kita tentukan panjang sisi AC dan untuk mempermudah dalam menentukannya, maka kita terlebih dahulu menentukan sisi depan, sisi miring, dan sisi samping dari segitiga itu. Adapaun penentuan sisi-sisi tersebut dapat digambarkan sebagai berikut.

Segitiga ABC

Untuk menentukan panjang sisi AC, kita dapat memanfaatkan perbandingan trigonometri pada sudut istimewa yaitu sin. Mengapa yang kita gunakan sin? Hal ini dikarenakan sisi yang diketahui adalah sisi AB dan yang dicari adalah sisi AC.

sin                    =  \(\frac{De}{Mi}\)

sin 30^o             =  \(\frac{AB}{AC}\)

\(\frac{1}{2}\)                     =  \(\frac{6}{AC}\)

1AC                =  2 ⨯ 6

AC                  =  12

Jadi, panjang sisi AC pada segitiga siku-siku ABC dengan siku-siku di B adalah 12 cm.

Contoh 2:

Hitunglah nilai dari cos 45^o tan 30^o + sec 30^o sin 60^o !

Penyelesaian:

cos 45^o tan 30^o + sec 30^o sin 60^o     

=  \(\left(\frac{1}{2}\sqrt{2}\right)\left(\frac{1}{3}\sqrt{3}\right) + \left(\frac{2}{3}\sqrt{3}\right)\left(\frac{1}{2}\sqrt{3}\right)\)

=  \(\left (\frac{1}{2}\times\frac{1}{3}\right)\left(\sqrt{2}\times\sqrt{3}\right) + \left(\frac{2}{3}\times\frac{1}{2}\right) \left(\sqrt{3}\times\sqrt{3} \right)\)

=  \(\frac{1}{6}\sqrt{6} + \frac{2}{6}\sqrt{9} \)

=  \(\frac{1}{6}\sqrt{6} + \frac{2}{6}\left(3\right) \)

=  \(\frac{1}{6}\sqrt{6} + \frac{6}{6}\)

=  \(\frac{1}{6}\sqrt{6} + 1\)

cos 45^o tan 30^o + sec 30^o sin 60^o     =  \(\frac{1}{6}\sqrt{6} + 1\)

Demikian penjelasan tentang perbandingan trigonometri pada sudut istimewa. Semoga materi ini dapat bermanfaat unttuk semua.